Klein Bottle Cartoons, Limericks, Rhymes, and Haiku

A Klein Bottle Cartoon by Jean-Pierre Petit

This is from Jean~Pierre Petit's le Topologicon -- a delightful book of adventures in topology. Alas, it's only in French. Jean Petit has worked extensively on Boy's Surface, and his series of books, Les aventures d'Anselme Lanturlu, tickle the mind and bring smiles to the eye. See http://www.jp-petit.org for more!

A Responsible Adult Says No to Non-Orientable Shapes

I don't know who modified this classic propaganda poster ... it once said (in Russian), "A responsible adult says NO to alcholic drinks"

 

Check out Glass Klein Bottles at Acme Klein Bottle's Home Page

 

 

Don't miss the 8-bit animation of an Acme Klein Bottle (done with the PICO-8 game engine, which renders motion as if it's on an antique Amiga computer!) Smiling graphics from game developer Mini Mech Media.

One sided verses & limericks: 

I like to live in my little Klein bottle.

Imagine a cylinder, stretched up'l and out'l.

Push in the bottom to link with the throttle.

You need 4 dimensions to bring this about'l.

A home that's ingenious, clever, and crafty.

I find it delightful, but a little bit drafty.

(apologies to Katharine O'Brien) 

 

A mathematician named Klein

Thought the Möbius Loop was divine

Said he, "If you glue

The edges of two

You get a weird bottle like mine."

 

This ray of from Edith Emeritz's brillaince:

I can tell by my friends' wondrous gazes

That my Klein Bottle truly amazes.

Some find my new phial

Outrageously vile,

It not only amuses, it crazes.

Deena Skolnick, Stanford University's Class of 2003 is happy with her Acme Klein Bottle:

 One day as I was sitting, merely resting at my work

There approached a friend of mine who first stared, then went berserk.

But since I'd learned in infancy that attention follows gaze,

I watched his eyes and saw they fell on a bottle to amaze.

It was, of course, none other than my Baby Classic Klein

A bottle without volume and with one side by design.

Quoth he, "Might I inquire, if I could be so bold,

As to where you have acquired this no-boundary manifold?"

"Why sure," said I, "it's no surprise, just look where you would think:

Who else could be behind this glass but Acme Bottles, Inc.?"

"Aha!" he cried and jumped for joy and rushed out and was gone

Leaving me to ponder my 3D phenomenon.

My friends, I have no moral with which to end this tale

Except to let you take a look at where they are on sale!

 

Joy Wartman has this to say:

A Mathematician named Cliff

Who found four dimensions terrif

Made bottles called Klein

That wouldn't hold wine

Should he try in dimension the Fifth?

Here's an unsolicited endorsement from Adrian Anderson who bought an Acme Klein Bottle in the summer of 2000:

Having received a bottle by Klein

An Acme product quite fine

If dimensionally able

I shall place on a table

And admire for a mighty long time

 

Andrea Blumberg tells us that::

A bottle, created by Klein,

Caused a fuss on both banks of the Rhine.

This miraculous flask

Spurred the people to ask,

"Can you do the same thing with a stein?"

 

Michele Denber writes::

I'm very happy to say

My Klein bottle got here today.

It's really quite fine,

This bottle by Klein

In an odd topological way.



 

This limerick by deepseajelly (July 2017):

On my desk I make use of cosine

I also love learning of Einstein

In need of dec'ration

And math-base elation

I purchased Acme's glass by F. Klein


Ben Eldred composed this limerick either on a breezy Houston morning or else at some other time in 2021:


An objet d'art that's quite bold,

This sparkling Acme manifold

     From the witty web store

     Filled with math jokes galore

I'll order before they're all sold!

... a few days later, Ben further polished his limerickal talents by scribbling:


My bottle arrived! I'm excited

To display my new art that's one-sided

     But it still hurts my brain

     WHen I try to explain

How it makes Mobius strips when divided!


Here's Cliff Stoll's attempt to riff on Lewis Carrol:

'Twas brillig in a manifold, where eigenvalues squirm,

A Klein bottle lurked without—defying every term—

And slick proofs did gyre about, as vectors through the field;

All twisty were the boundaries, where edges would not yield.

“Beware the foldless flask,” they said, “the Acme of its kind—

It drinks its own domain and loops through every mind.

No inside/outside, yet form persists—defying what seems true—

A vessel made of paradox the mind must wander through.”

Cliff took his torch in hand, in fractal thought so deeply caught,

Through Möbius dreams and genus schemes, in boro glass he wrought;

Till standing there, with knowing grin, he sealed that looping seam—

A surface where all sides are one, like logic in a dream.

“And hast thou mapped the Klein, my friend?” the silent blackboard asked.

“Oh yes,” he said, “but not in space where Euclid’s tidy rules hold fast.

For here, the world folds back on self—no edge to make it real—

Just mathematics, pure and strange, where nonsense truths congeal.”

From: "-s-p-e-c-t-r-u-m-"

Thinking in 4-D is hip,

But it gives my poor braincells a trip.

So I think that I ought'l

Leave Klein to his bottle;

I'll just stick with Moebius' strip.

 

To add to dimensions one more,

You just square what you had before.

So if I've got it straight

That the strip's figure-eight,

Is Klein's figure then sixty-four?

Alex Rennet (of McMaster Univ) has a poetic father:

There once was a physicist who made bottles topological,
whose surfaces defied all the senses logical;
One day in pursuit of dimensions unattainable,
using all the strength of which he was capable,
he blew so hard, one turned insideoutical.

Chris Innanen (aka Nonsanity) writes:

"This fleaker's no leaker," Roy fessed
"But all thickened solutions congest.
But decanting is quick
With no 'insides' to stick
So an Erlenmeyer Klein bottle's best!"

This one by Peter Beuret:

There once was a bottle called Klein

That had such a clever design

It would turn inside out,

Which created some doubt

When it came to decanting the wine.

 

Bill Kilner's contribution to nonorientable poetry::

When a Klein Bottle's blown out of glass
(Like a flat drawing of Mobus class)

Since the object's 4-D
If you crush it to 3

Then the cross-overs pierce where they pass.

A Haiku by Jacob and Shari Bandes:

In 4 dimensions

there is no intersection

but in 3 there is.

 

Fraser Talbot of Christchurch, NZ created this singularly accurate Haiku:

Two Moebius loops

Combine to form this bottle

With only one side.

 

Ode on a Klein Bottle

by Edith Emeritz, With sincere apologies to Keats

Thou perfect unspoiled borosilicate manifold,
Thou alien sojourner from dimension four,
Crystal visitor, who canst thou behold
A transparent image more puzzling than before:
What Mobius loops haunt about thy fringe
Of self-intersection, or of neck,
Twisted in nonorientability?
What curves or bends are these? What aura check?
What mad pursuit? What effort to unhinge?
What zero volume vial? What wild ecstasy?

 

Arrival of My Klein Bottle

by RAD Donato

I thought that I might haversine,
but then I figured, nope,
since she was neither in nor out,
immersed in visions of
manifold lemniscate
R four projections of
beautiful
spirals of Cote


I thought then I might sine myself,
when Ida surfaced later,
she wanted one too, in just four hues,
and one like an overfed
eyes of pink
albino
cannibal blind
alligator.


We then went out to celebrate
the film "Paradromic" was playing,
reviewers had written that "so many twists,
left the viewers in knots
and ringing in ears
and chair surfaces
hardly remaining"


The theater first showed us Mobius shorts,
but this held no interest for I,
the movies were all simple one-sided plots,
full of holes
and worse
she made me watch twice
'cause she likes some n 2-tori.


I somehow was able to watch the hole movie,
though many times made sounds quite glottal,
needless to say I hurried right home
so I could go hit the Klein Bottle.

 

The following by Cliff Stoll:

Acme's Klein Bottl

Looks a lotl

Like a big ol'

Axolotl

 

The space it takes'll

Needs a tunnel

With a hole

Like a funnel.

 

Its Singularities'll

Make a circl

In it's space'l

Poly-dimensional.

 

Its sides be singl

Like its handl.

This twisty thing'l

Moebius Band'l

An Acme Manifold'l

Keep you out of troubl

 

This boundless bottl

Isn't awfl

Spheres with crosscaps

Homeomorph'll

...Cliff Stoll 10/2000 (with apologies to David McCord)

 

Mathematicians try hard to floor us

With a non-orientable torus

The bottle of Klein

They say is divine

But it is so exceedingly porus.

 

from the Space Child's Mother Goose by Winsor & Parry (a whimsical 1950's book, recently republished by Purple House Press) :

Three jolly sailors from Blaydon-on-Tyne

They went to sea in a bottle by Klein.

Since the sea was entirely inside the hull

The scenery seen was exceedingly dull.

Oliver Humpage of Bristol, England wrote these two haiku after receiving an Acme Klein Bottle:

bottle of one side

holds nothing and ev'rything;

no one understands

when filled with water,

this four-dimensioned vessel

would leak in odd ways

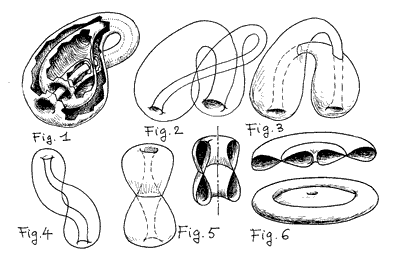
Jean-Pierre Petit has designed some wonderful new Klein Bottle derivatives, seen in his paper, TOPOLOGIE- Le retournement non trivial du tore. (C.R. Acad. Sc. Paris t. 287, 20 November 1978). Here are a few figures from this brilliant mind. Note that these are not Klein bottles - as far as I can tell, each is homeomorphic to a torus. Figure 4 is very much like the Acme double "Klein bottle" (which is really a torus, not a Kleinbot).

Annie Giercyk of Muhlenberg College wanted to fill a baby Klein bottle - she found that Nerds Candies will do the trick!

Nerds in a Klein bottle

 

 Send your contributions or links to kleinbottle(AT)kleinbottleDOTcom

Acme Klein Bottles - Exclusive Purveyors of the Non-Orientable

Return to Acme's Home Page